On a college visit with my high school son to Rose Hullman in Terre Haute, IN I picked up a copy of the schools’s alumni magazine. The magazine had a section of brain teasers and logic problems written by Herb Bailey. One of the brain teasers was interesting to me since it was a challenge to write an algorithm to identify a specific number sequence called a “curious” sequence. The brain teaser was as follows:

To solve this brain teaser I had to fully understand the rules of the sequence. After analyzing the sequence, I had an idea that a curious sequence can be defined by two characteristics. First the sequence equals n+1 when summed up. So for n =3 for example, 2+0+2+0 = 4. The second part is that each position reveals the number of digest in the sequence when referencing as an array with an index. This is demonstrated below.

Notice how if the sequence is treated as an array and how each element of the array can be referenced by an index number. So for the first element of the array when the index=0, the value is 2. 2 also represent the number of zeros present in the array. Moving to the next element where the index=1 shows a value of 0. Interesting enough there are zero 1s in the sequence of 2020. Pretty clever to say the least!
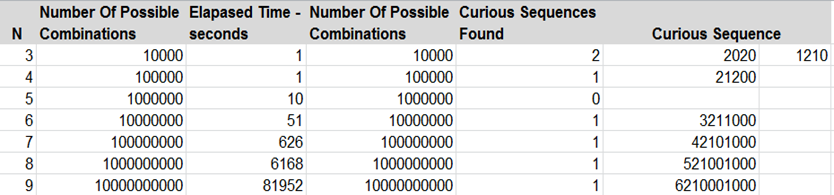
Now that I got a clearer understanding of the problem the question becomes, can algorithm can be created that can identify all curious sequences when n=4, but also when n=5, n=6, n=6….? As it turns out it is very possible to develop an algorithm that will identify curious sequences in a linear time complexity. I used Perl to impliment a solution. The results for n=3 to n=9 are shown below.